수학 속 숨겨진 실생활의 해답, 이차함수를 만나보세요! 일상 속에서 이차함수가 어떻게 사용되는지, 그리고 그것이 우리의 문제 해결에 어떻게 도움이 되는지 그리고 물리학에서 경제학, 금융에 이르기까지, 이차함수의 실용적인 면모를 발견하는 여정에 함께 하실 준비가 되셨나요? 자 그럼 시작해 볼까요

이차함수의 정의와 특성
| 항목 | 수식 | 설명 |
| 일반형 | \(f(x) = ax^2 + bx + c\) | 표준 이차함수 형태 |
| 꼭짓점 형태 | \(f(x) = a(x-p)^2 + q\) | 꼭짓점이 (p, q)인 이차함수 형태 |
| 그래프의 볼록 유형 | \(a > 0\) 아래로 볼록 \(a < 0\) 위로 볼록 |
계수 a의 부호에 따라 그래프의 볼록 방향이 결정됨 |
| 그래프의 폭 | \(|a|\)의 값이 클수록 폭 감소 \(|a|\)의 값이 작을수록 폭 증가 |
계수 a의 절대값 크기에 따라 그래프의 폭이 달라짐 |
| 대칭축 | \(x = p\) 또는 \(x = -\frac{b}{2a}\) | 이차함수 그래프의 대칭축 위치 |
| x절편 | 해당하는 근의 공식 적용 | \(a \neq 0\)일 때 x절편이 존재하며, 근의 공식을 사용하여 계산 |
| y절편 | \(c\) 또는 \(ap^2 + q\) |
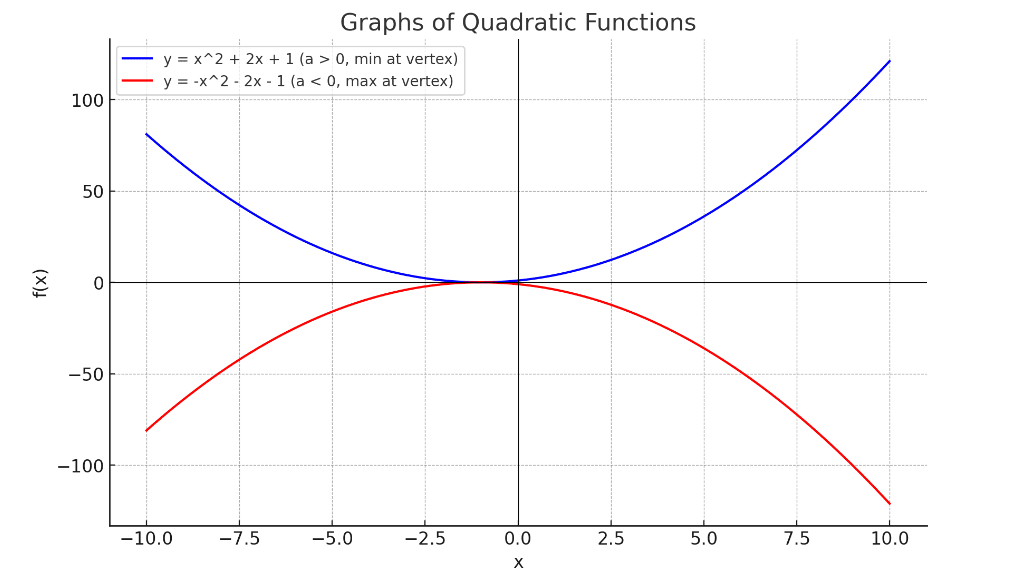
이차함수란, 주어진 식 𝑓(𝑥)=𝑎𝑥2+𝑏𝑥+𝑐f(x)=ax 2+bx+c (여기서 a ≠ 0)의 형태로 나타나며, 그래프는 특유의 포물선 형태를 띕니다. 이차함수 그래프의 중요한 특징 중 하나는 꼭짓점을 통해 함수의 최소값 또는 최대값을 알 수 있다는 것입니다. 만약 a가 양수라면 포물선은 위로 볼록(아래쪽에 꼭짓점), a가 음수라면 아래로 볼록(위쪽에 꼭짓점) 형태를 띕니다. 이런 특성 때문에 최적값을 찾거나 결과를 예측하는 데 유용하게 사용됩니다.
물리학에서의 이차함수 탄도학의 예
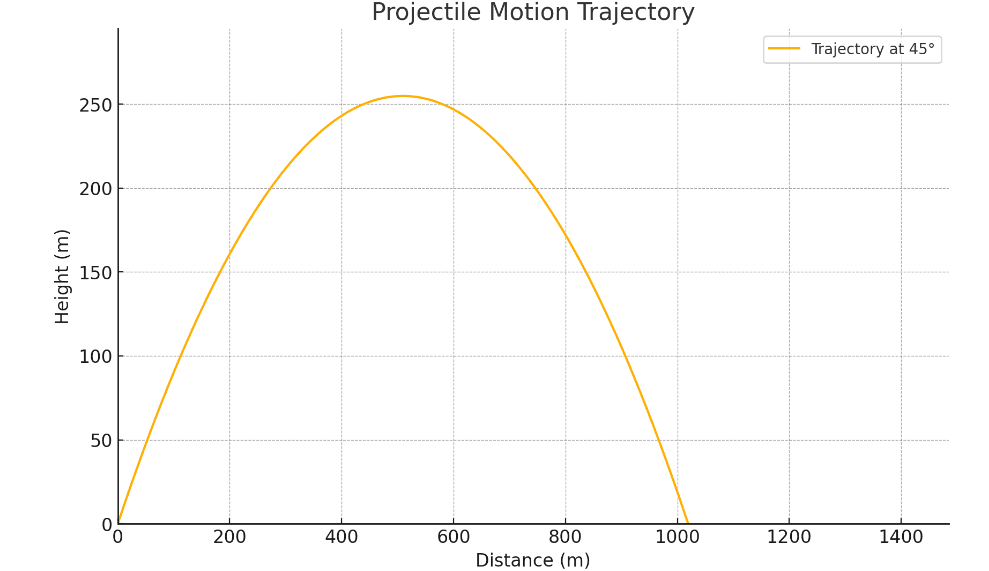
물리학, 특히 탄도학에서는 이차함수가 매우 중요합니다. 발사체가 공중을 날아가는 궤적은 대표적으로 이차함수로 모델링됩니다. 로켓이나 포탄을 발사할 때, 발사 각도와 초기 속도가 주어지면, 이차함수를 사용해 최종적으로 목표 지점에 도달할 위치를 정확하게 예측할 수 있습니다. 이러한 계산은 안전하고 정확한 발사를 위해 필수적입니다.
경제학적 접근 수요와 공급 곡선
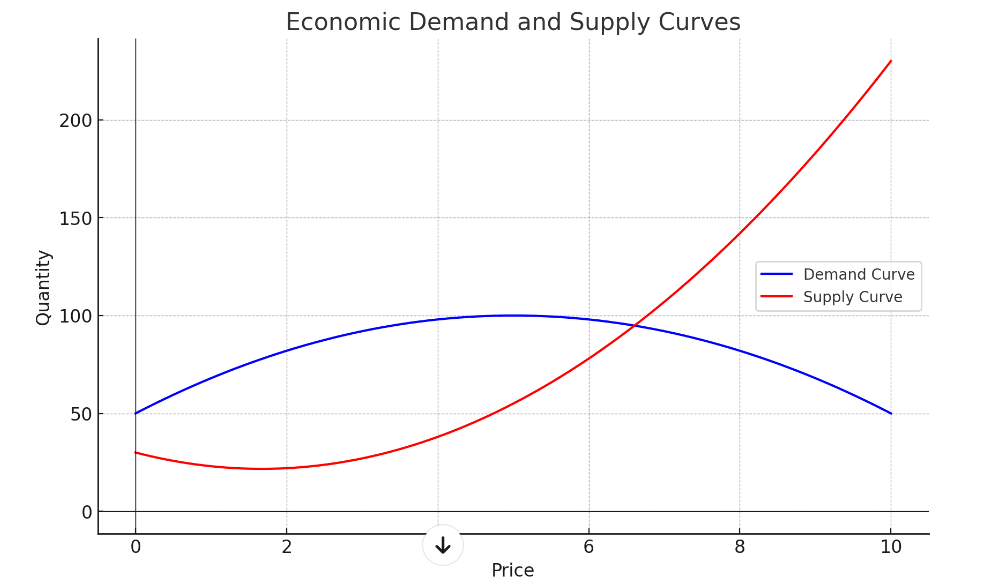
경제학에서는 수요와 공급 곡선을 분석할 때 이차함수를 사용합니다. 시장에서의 가격과 수요 양에 대한 변동을 예측하고 분석함으로써, 기업이나 정책 결정자가 최적의 가격과 생산량을 결정할 수 있도록 돕습니다. 예를 들어, 가격이 상승함에 따라 수요가 어떻게 변하는지를 파악하고, 이 정보를 바탕으로 공급 계획을 세울 수 있습니다.
올 9월 역대급 기능을 탑재하고 출시 된다! 사전 예약으로 아이폰16을 먼저 만나보세요!
아이폰16 사전예약
아이폰16 사전예약 사은품 아이폰16pro 디자인 미니 아이폰16 색상 가격 c타비 그린 아이폰16 프로 디자인 스펙 출시일 아이폰 프로 자급제 PRO 프로 자급제 스펙 쿠팡 아이폰16 사전예약 홈페이지
epostphone.kr
공학에서의 응용 파동 및 진동 분석
공학 분야, 특히 구조물의 진동 분석에 이차함수는 필수적입니다. 다리나 건물 같은 구조물에서 발생할 수 있는 진동을 분석하고 예측하는 데 이차함수가 활용됩니다. 이를 통해 구조물의 안전성을 평가하고, 필요한 경우 보강 조치를 취할 수 있습니다.
대박 게임 총출동! 다양한 게임을 만나보세요~ 신개념 맞고 부터~!
피망 - 대한민국 No.1 게임포털 피망!
피망 뉴맞고, 피망 포커, 브라운더스트 등 추천 모바일게임과 FPS, 스포츠, 웹게임, RPG 등 다양한 온라인 PC게임을 확인해 보세요!
www.pmang.com
컴퓨터 그래픽과 게임 디자인에서의 활용
비디오 게임 개발이나 애니메이션 제작에 있어 컴퓨터 그래픽 분야에서도 이차함수가 중요합니다. 캐릭터나 객체의 움직임을 자연스럽고 실감 나게 표현할 때 이차함수를 활용합니다. 예를 들어, 물체가 던져졌을 때의 궤적이나 점프하는 동작 등이 이차함수의 형태로 계산되어 그래픽스에서 묘사됩니다. 이를 통해 보다 사실적이고 매끄러운 애니메이션 효과를 구현할 수 있습니다.
미스트롯3 투표방법
미스트롯3 투표하기 미스트롯3 투표, 실시간 투표, 문자 투표, 미스트롯3 투표하기 방법, 인기 투표 사이트 홈페이지, 대국민 응원투표 준결승 결승 투표 문자번호
sainthome.kr
금융 분야에서의 이차함수 활용 옵션 가격 산정
금융 시장에서는 옵션 거래 시 옵션 가격 산정에 이차함수가 사용됩니다. 주가의 변동성과 만기까지의 기간을 고려하여 옵션의 가치를 계산하는 데 이차함수를 활용하면, 보다 정확하고 효과적인 투자 결정을 내릴 수 있습니다
마무리
이차함수는 우리의 일상과 밀접하게 연결되어 있습니다. 물리학, 경제학, 공학, 컴퓨터 그래픽, 금융 등 다양한 분야에서 이차함수를 이해하고 활용함으로써 보다 효율적이고 경제적인 해결책을 도출할 수 있습니다. 이러한 다양한 적용을 통해 이차함수의 원리를 배우고, 실제로 적용해 보는 것은 우리의 문제 해결 능력을 크게 향상시킬 수 있습니다.
이차함수의 깊은 이해는 창의적인 문제 해결뿐만 아니라 효과적인 의사결정에도 중요한 역할을 합니다. 다음에 마주하는 문제에 이차함수를 적용해 보세요. 놀라운 결과를 얻을 수 있을 것입니다.
행복한 학습과 성공적인 적용을 기원합니다!
'여행' 카테고리의 다른 글
| 틱톡라이트 출금한도 와 계정삭제 한방 정리 (0) | 2024.05.13 |
|---|---|
| 맥북을 넘어선 아이패드 프로 최첨단 애플 M4칩 탑재 공개 (0) | 2024.05.09 |
| 이차함수 실생활 활용 및 최대 최소 값 쉽게 찾기 (0) | 2024.05.09 |
| 아이폰 16 새로운 카메라 비디오 풍부한 컬러와 저장 공간 기능 (0) | 2024.05.07 |
| 산요작티 C4 빈티지 카메라 디자인 화소 촬영모드까지 총정리 (0) | 2024.05.07 |